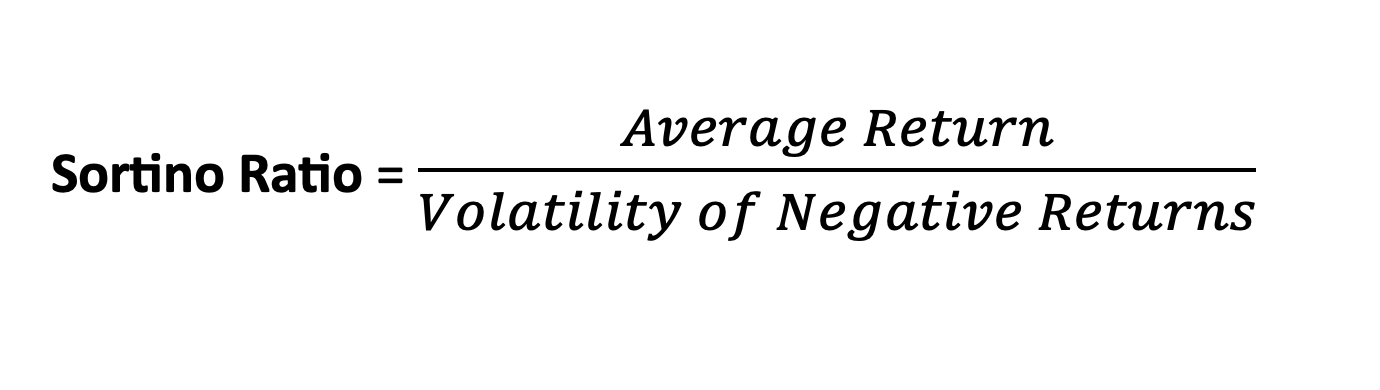Abstract
Building on the portfolio optimization strategies established in our foundational research, titled (Optimizing Portfolio Performance: A Comprehensive Approach with Swing Trading, Asset Allocation, and Enhanced Lazy Portfolio)., and its subsequent application to UCITS ETFs within the European market, this paper seeks to transpose and evolve these strategies within the Australian financial context, utilizing Australian ETFs. As we did with the UCITS (Bridging Portfolio Strategies: From USA ETFs to UCITS ETFs), our objective is to align these strategies with the Australian market's distinct attributes and oversight.
Australian ETFs offer a spectrum of investment opportunities in local equities, bonds, commodities, and currencies, tailored to comply with the stringent Australian financial regulations that prioritize investor protection, liquidity, and transparency. This study endeavors to replicate the original strategies and, by extension, the UCITS ETF approach [insert link to UCITS paper here], while also constructing and analyzing two distinct portfolios that calibrate capital distribution to improve the overall risk-reward profile, with an aim to mitigate drawdowns and preserve performance. We seek to delineate the Optimal Efficient Frontier portfolio that emerges from these refined strategies, providing a meticulous assessment of the resulting metrics within the Australian market.
Introduction
In the Australian investment sphere, where managed funds and superannuation schemes are prevalent, there has been a growing trend towards using ETFs for both retail and institutional investing. The Australian ETFs, while mirroring the adaptability and broad market access of their global counterparts, are uniquely calibrated to meet the local financial regulations and investment climate.
In this study, we replicate and refine the strategies from our prior research, utilizing ETFs that are compliant with Australian regulations. Our focus will remain on Swing and Lazy Portfolio strategies, considering the extensive and varied range of Australian ETFs available for Asset Allocation. Our analysis spans from January 1, 2009, to the present, a period that aligns with the rise in availability and popularity of ETFs in Australia.
Our goal is to enhance portfolio performance for the Australian market by balancing returns with volatility management. The forthcoming sections will present an in-depth analysis of our findings, focusing on portfolio optimization in the context of Australian ETFs.
Study Limitations
This study is subject to specific limitations:
- Adaptability to AUD ETFs for U.S. ETFs Strategies: While the original portfolio employed Swing Trading, Asset Allocation, and Lazy Portfolio strategies, the extensive ETF range required for Asset Allocation is not compatible with the UCITS framework. Hence, this study is focused on adapting and analyzing the Swing and Lazy Portfolio strategies within UCITS constraints.
- Data Availability Constraints: Our analysis is limited to the period from January 2015 to December 2023. This limitation is due to the unavailability of comprehensive AUD ETF data prior to January 2015, necessary for accurately replicating the original strategies.
The research, therefore, utilizes AUD ETFs to implement the Swing and Lazy Portfolio strategies from January 1, 2015, to November 30, 2023, aiming to optimize portfolio performance by minimizing volatility without significantly impacting returns.
The mapping of original U.S ETFs to AUD equivalents is as follows:

Strategies AUD ETFs
In this paper, we detail the adaptation of the original algorithm to align with AUD ETFs. The backtesting of these strategies and the portfolios, which will be discussed later in this paper, was conducted over a specified period using Amibroker, a sophisticated analytical tool. This paper includes a series of figures that display the outcomes of these backtests. Additionally, a Python script was developed to generate metrics that are not available in Amibroker.
Swing:
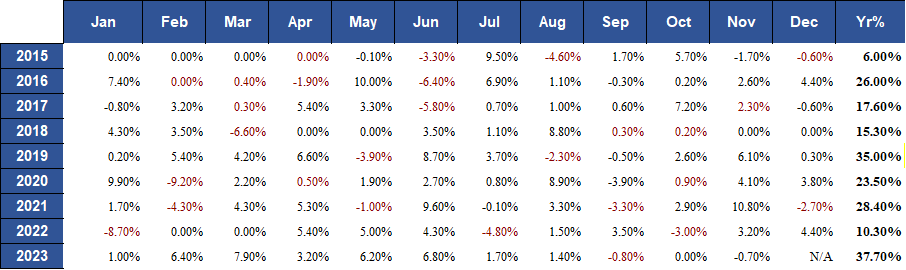
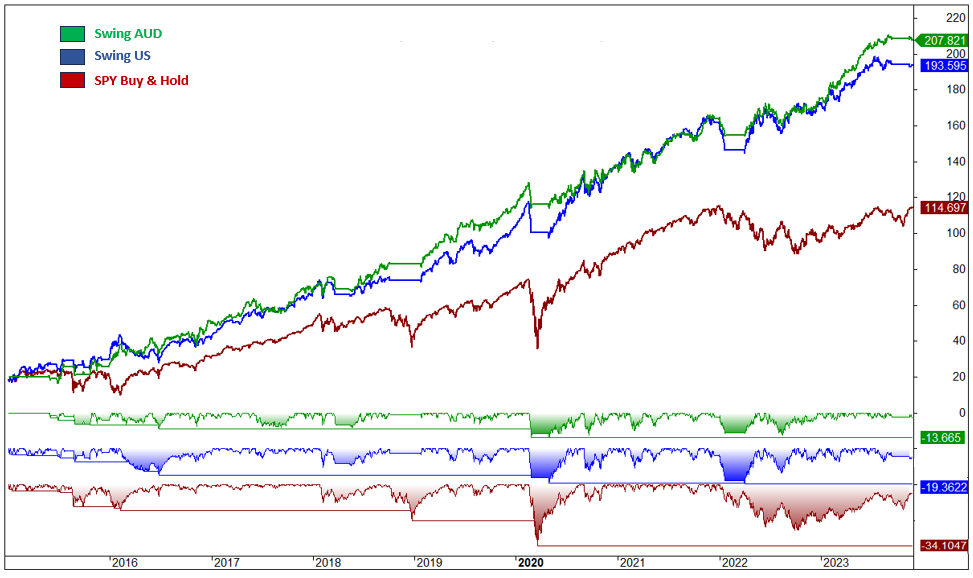
The Swing strategy, applied to AUD ETFs, consistently surpassed the S&P 500, yielding positive annual outcomes with managed drawdowns. Compared to the US ETFs variant, it achieved superior performance and nearly 3% less maximum drawdown. The AUD ETFs strategy also showed reduced volatility, coupled with enhanced Sharpe and Sortino ratios, reflecting a more favourable risk-reward balance. Additional insights and comprehensive metrics illustrating these achievements will be detailed in an imminent figure.
Fig.1: Swing AUD ETFs monthly and annual returns
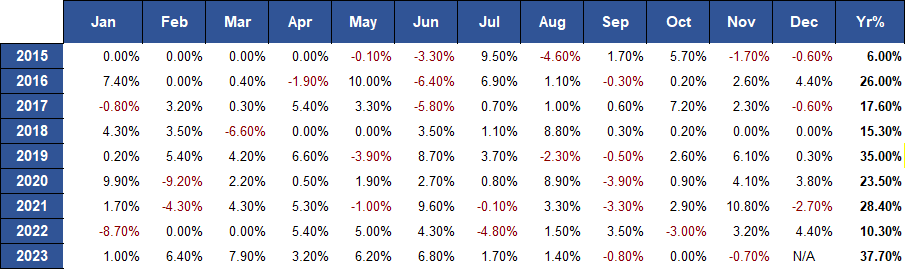
Fig.2: Swing U.S ETFs monthly and annual returns for same period
The following illustration presents key metrics for the Swing strategy when implemented with AUD ETFs and for the Swing strategy using USA ETFs, with SPY serving as a benchmark for comparison. For detailed information on the calculation methods of these metrics, please refer to Annex I.
Fig. 3: Key Metrics Comparison - Swing AUD Strategy vs. Swing USA Strategy and SPY (Benchmark)
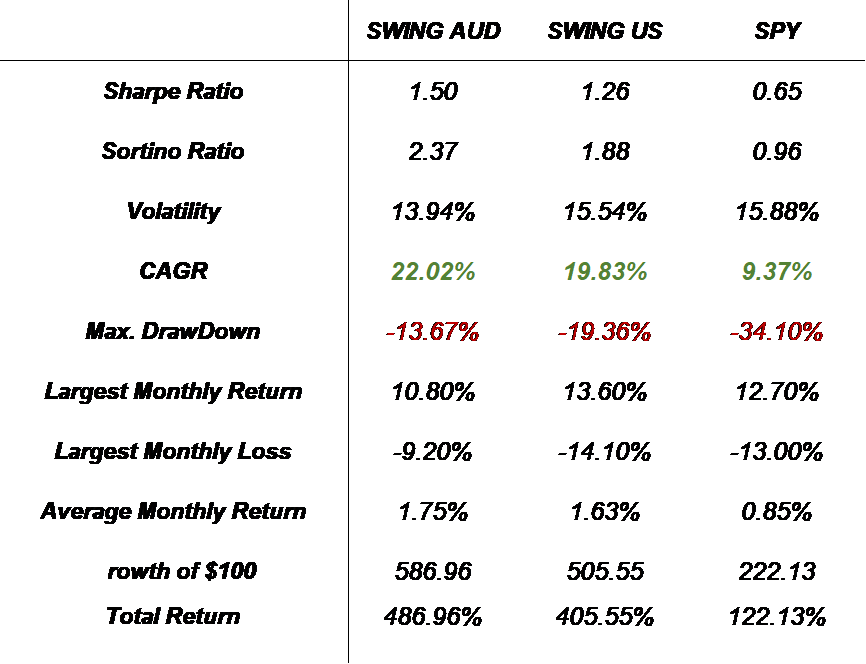
Fig. 4: Cumulative Returns and Drawdown Comparison - Swing AUD Strategy vs. Swing USA Strategy and SPY (Benchmark)
Lazy Portfolio:
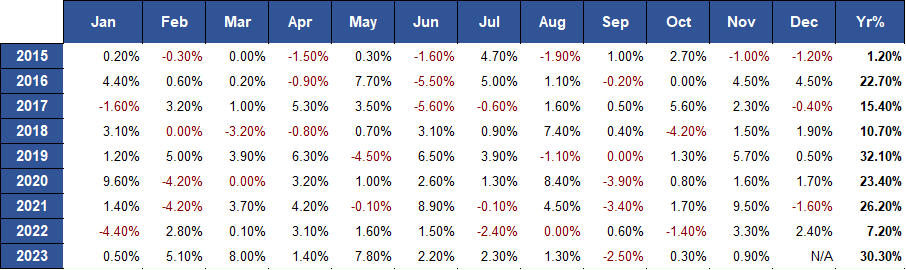
The Lazy Portfolio strategy employing AUD ETFs outshined the S&P 500 benchmark with higher annual returns while maintaining a similar performance to its US ETFs equivalent in terms of returns and drawdown. Although the AUD version displayed a slightly higher volatility compared to the US ETFs, both versions showcased a comparable risk-reward profile. A forthcoming figure will provide further insights and detailed metrics to elaborate on the comparative performance of the AUD implementation.
Fig.5 Lazy Portfolio AUD monthly and annual returns
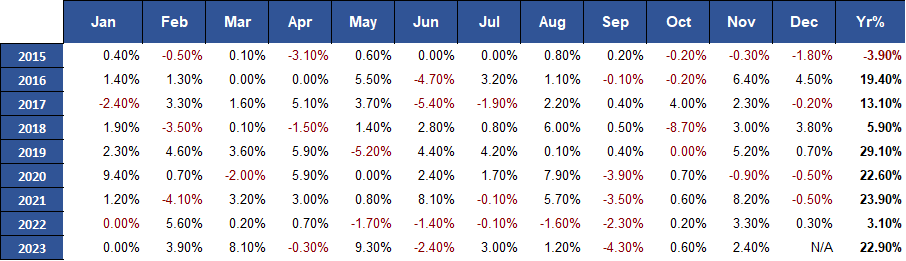
Fig.6 Lazy Portfolio USA monthly and annual returns
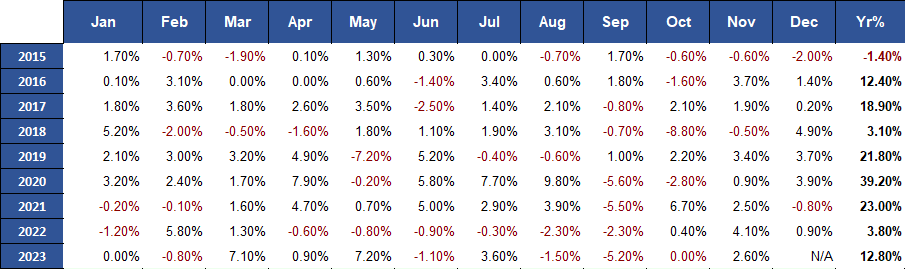
The following illustration presents key metrics for the Lazy Portfolio strategy.
Fig. 7: Key Metrics Comparison – Lazy Port AUD Strategy vs. Lazy Port USA Strategy and SPY (Benchmark)
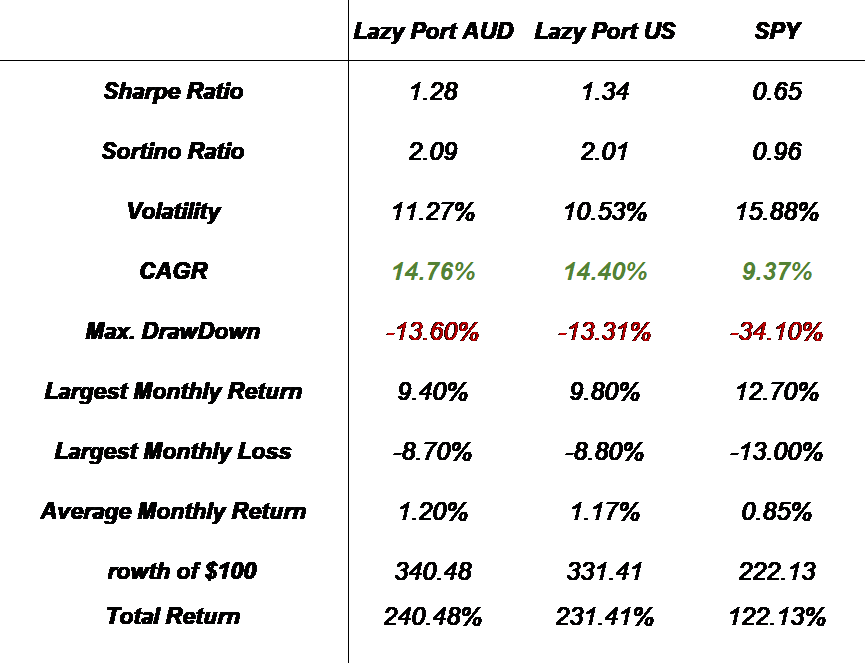
Fig.8: Cumulative Returns and Drawdown Comparison – Lazy P. AUD Strategy vs. Lazy P. USA Strategy and SPY (Benchmark)
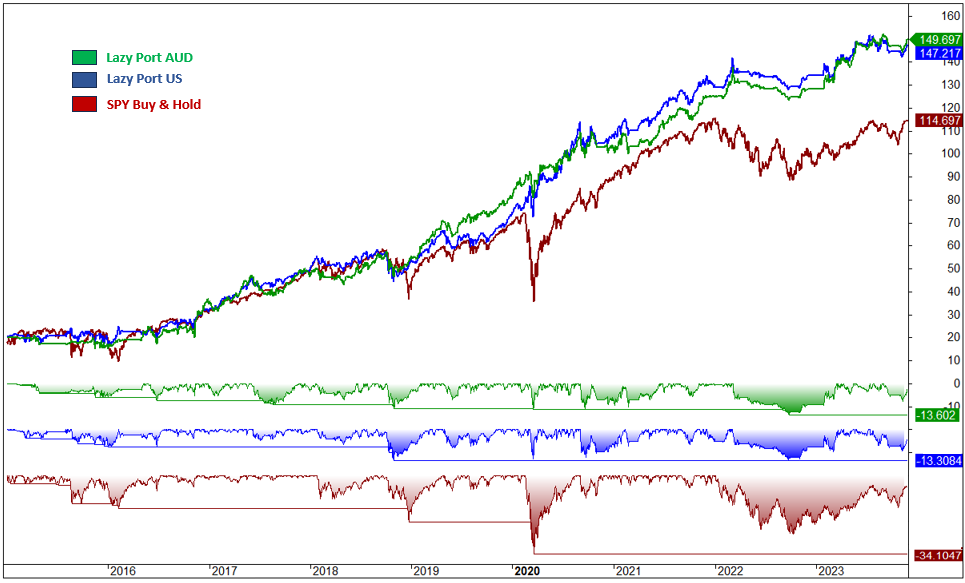
In summary, our analysis of the Swing and Lazy Portfolio strategies using AUD ETFs indicates impressive outcomes. Both strategies have exceeded the S&P 500 in terms of returns, effectively managing drawdown. Specifically, the Swing strategy with AUD ETFs mirrors its U.S. ETFs performance, reflecting its adaptability and effectiveness. Additionally, the Lazy Portfolio with AUD ETFs outperformed the U.S. ETFs variant, delivering higher returns with better risk management, evidenced by lower drawdown and volatility. These findings suggest that employing AUD ETFs can be advantageous for sophisticated portfolio management in the Australian context, with both strategies demonstrating similar risk-reward dynamics.
In subsequent sections, our paper will explore portfolios combining these strategies in varying allocations, specifically focusing on the (50-50) and (70-30) mixes. Additionally, We aim to identify the most efficient portfolio mix on the Efficient Frontier and to compare the risk-reward profiles of the combined strategies. This comprehensive analysis is intended to provide deeper insights into the interplay between the strategies and their collective capacity to optimize risk-adjusted returns in diverse portfolio compositions.
Portfolios 50-50 and 70-30
This section focuses on analyzing two distinct portfolios, each with a unique combination of strategies:
- Portfolio 50-50, evenly split with 50% Swing strategy and 50% Lazy Portfolio.
- Portfolio 70-30: comprising 70% Swing strategy and 30% Lazy Portfolio.
Our methodology involved using Amibroker to harness equity data from both strategies. We implemented the specified allocations and conducted monthly rebalancing to accurately mimic the strategies' real-world performance, particularly addressing the Lazy Portfolio's rebalancing needs. To address any gaps in Amibroker's output, we supplemented our analysis with custom Python scripts, allowing for a more comprehensive metric assessment.
The results:
AUD Portfolio 50-50:
The upcoming figures will illustrate that the Portfolio 50-50 not only reduces drawdown compared to the Swing strategy, suggesting a more conservative approach to capital preservation, but it also provides higher returns than the Lazy Portfolio. In fact, the Portfolio 50-50 experiences a lower maximum drawdown than both the Swing and Lazy Portfolios, demonstrating its effectiveness in mitigating risk. With volatility matching that of the Lazy Portfolio, the Portfolio 50-50 maintains stability in investment performance. This strategic balance results in a risk-reward ratio that is favourable, balancing prudent risk management with solid returns. The forthcoming visual presentation will detail these metrics more extensively.
Fig. 9: AUD Portfolio 50-50 Monthly and Annual Returns
AUD Portfolio 70-30:
Portfolio 70-30 exhibits a nominally greater drawdown than Portfolio 50-50. However, it compensates with a substantially higher annual return, which might be attractive to investors with an appetite for moderate risk. The increment in volatility, although present, does not exceed conventional thresholds, suggesting that the enhanced performance could be an acceptable trade-off for the slightly elevated risk. This nuanced increment in risk is potentially justified by the performance uplift, offering a compelling case for those assessing risk-return dynamics within their investment strategy. Detailed information on the risk-reward ratio for Portfolio 70-30 will be provided in an upcoming figure, highlighting key metrics.
Fig. 10: AUD Portfolio 70-30 Monthly and Annual Returns
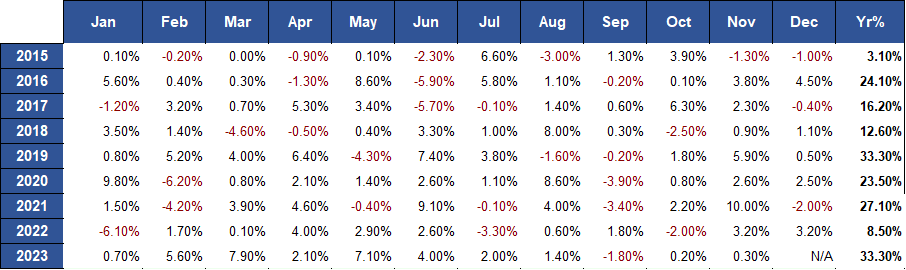
Fig. 11: Comparison of Key Metrics – AUD Portfolio 50-50 and AUD Portfolio 70-30 vs. SPY (Benchmark)
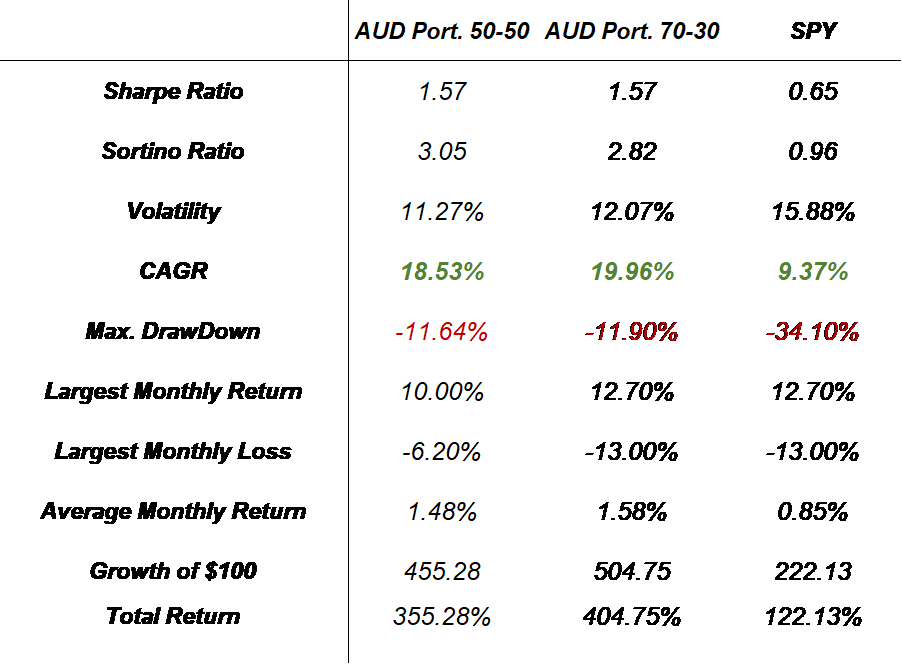
Fig. 12: Comparison of Cumulative Returns and Drawdown – AUD Portfolio 50-50 and AUD Portfolio 70-30 vs SPY (Benchmark)
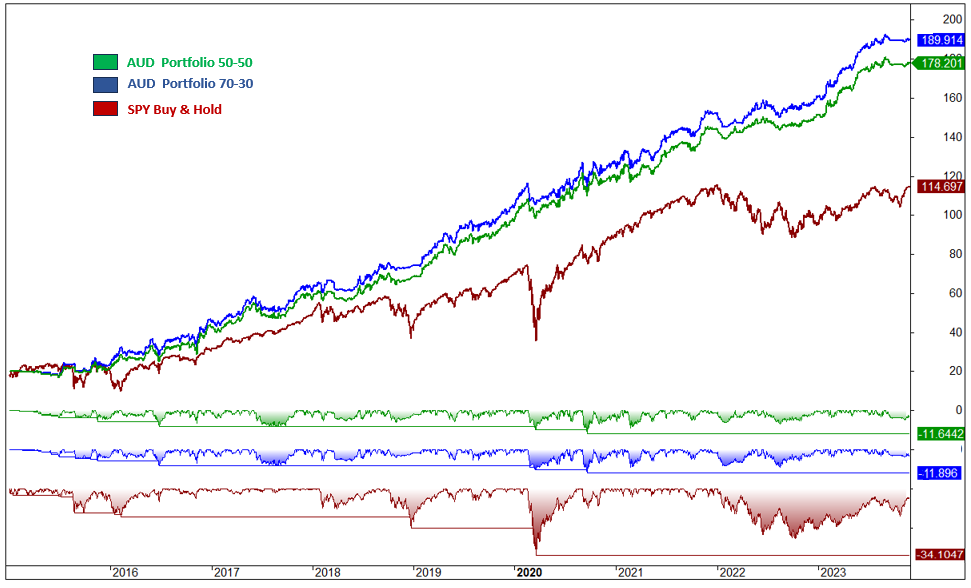
The Portfolio 50-50, which equally merges the Swing and Lazy Portfolio approaches, demonstrates an effective reduction in drawdown when compared to the Swing strategy, concurrently delivering superior returns relative to the Lazy Portfolio. It notably achieves a lower maximum drawdown than both the Swing and Lazy Portfolios, affirming its capacity for risk mitigation. Mirroring the volatility of the Lazy Portfolio, the Portfolio 50-50 offers investment stability. This equilibrium results in an advantageous risk-reward ratio, marrying cautious risk management with satisfactory returns.
Conversely, the Portfolio 70-30, leaning more towards the Swing strategy, incurs a slightly higher drawdown and a modest increase in volatility relative to the Portfolio 50-50. Nevertheless, it offers a markedly higher annual return, presenting a potentially attractive proposition for investors who are comfortable with moderate increases in risk. The higher performance of Portfolio 70-30 may warrant the incremental risk, presenting an intriguing option for those evaluating the trade-offs inherent in risk-reward optimization.
Each portfolio exhibits unique attributes, with the Portfolio 50-50 distinguished by its balanced approach. The next section of this paper will identify the optimal Efficient Frontier portfolio composition within the AUD ETF framework. This will include a comprehensive assessment of metrics and risk-reward profiles for each strategy and their combined portfolio forms.
Optimal Efficient Frontier:
In this section of our study, we aim to construct a portfolio that achieves the optimal distribution of strategies by applying the principles of the Optimal Efficient Frontier.
The Optimal Efficient Frontier, a fundamental concept in modern portfolio theory developed by Harry Markowitz, illustrates the trade-off between portfolio risk and return, with the goal of maximizing the Sharpe ratio. It identifies efficient portfolios that either maximize expected return for a given risk or minimize risk for a set return, with a focus on maximizing the Sharpe ratio, a metric of risk-adjusted return. Portfolios positioned on this curve represent optimal efficiency, providing the highest possible return for a given level of risk, in line with the objectives of investors. This involves analyzing assets' expected returns, variances, and covariances to construct portfolios that enhance the Sharpe ratio.
To compute the optimal frontier, we employed monthly returns data for the strategies and generated the calculations and accompanying graph using a Python script.
The following graph represents the Efficient Frontier simulations. The point marked with a red star (Tangency Portfolio) indicates the optimal portfolio on the Efficient Frontier, comprising a combination of the Swing and Lazy Portfolio strategies that achieves the highest Sharpe ratio.
Fig. 13: Efficient Frontier Simulation
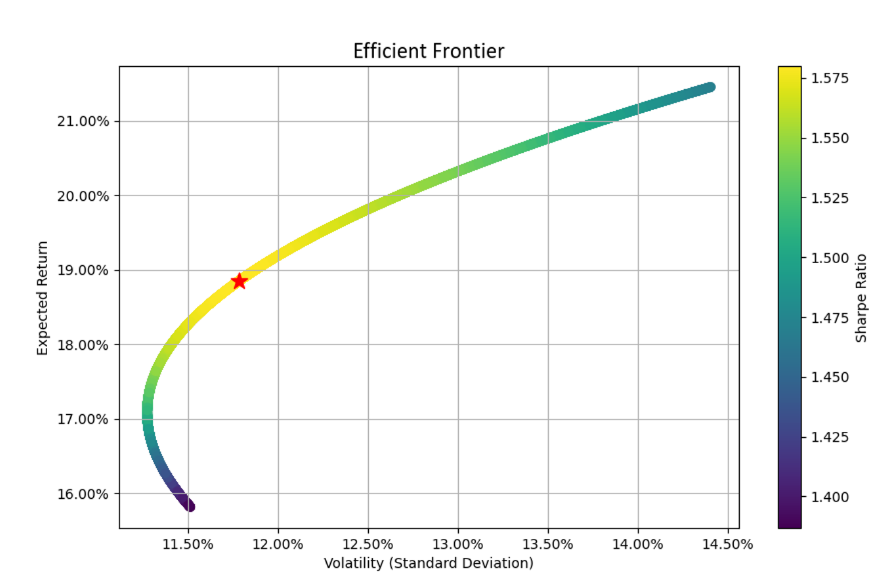
As highlighted by the red star in the above graph, the composition of the Optimal Efficient Frontier portfolio is as follows:
- Swing: 51%
- Lazy Portfolio: 49%
In this case the Portfolio 50-50 is close to the optimal efficient frontier. The calculation of the optimal frontier portfolio is based on the entire dataset provided, spanning from 2015 to 2023. It is advisable to periodically recalculate the Optimal Efficient Frontier and adjust the portfolio weights accordingly. The frequency of these recalculations and adjustments should be based on various factors, including prevailing market conditions, the chosen investment strategy, and the investor's risk tolerance and investment horizon.
General recommendations for recalibration are as follows:
Active Management Approach: For those adopting an active management style, a review every quarter or semi-annually is typically recommended.
Passive Management Approach: For investors with a more passive strategy, an annual review is generally sufficient.
Ultimately, the decision to rebalance should be in line with the overarching investment strategy, carefully weighing the costs and benefits. Consulting with a financial advisor can be advantageous to customize the approach to suit individual needs and adapt to changing market conditions.
Below are the metrics for all the portfolios and the strategies.
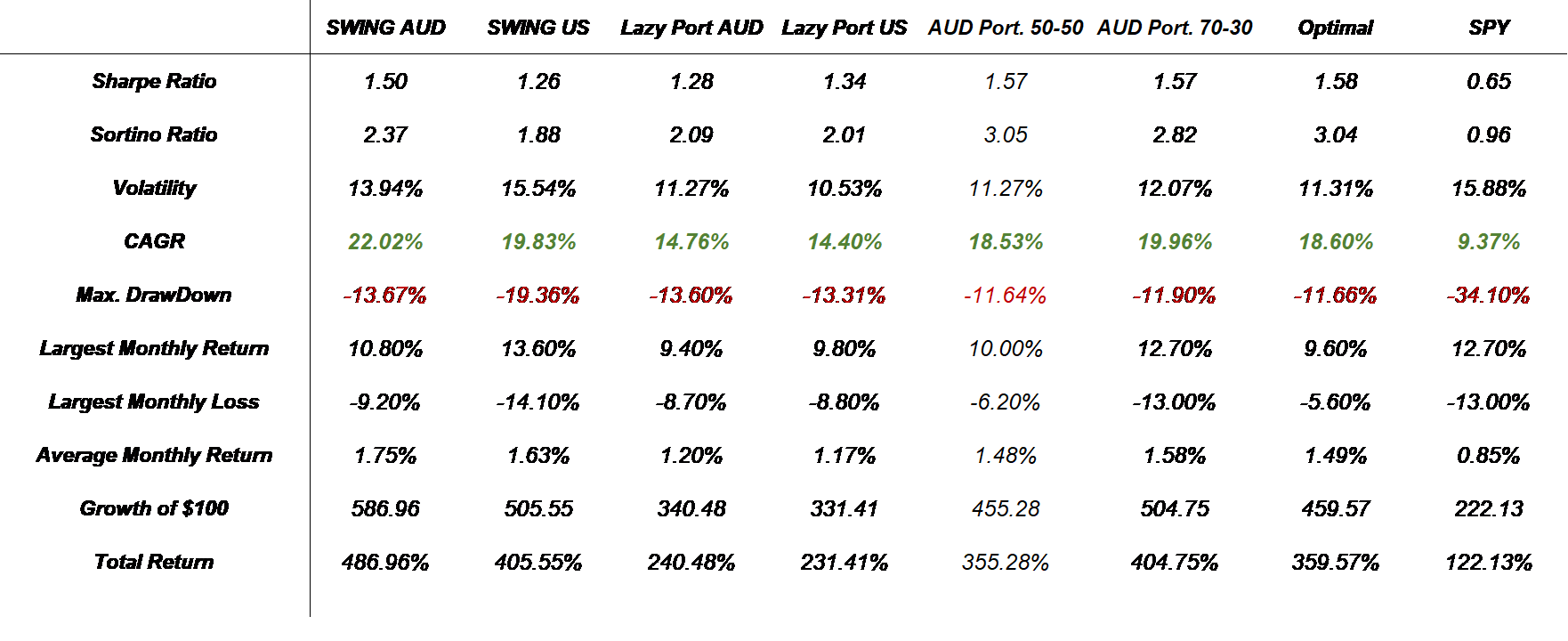
Risk-Reward Analysis:
The graph presented below provides a comprehensive representation of various strategies and portfolios, plotted based on their risk-reward profiles. On this graph, the x-axis denotes Volatility, serving as a measure of risk, while the y-axis represents the Expected Returns, indicating the potential reward. This analytical tool compares all the strategies based on their respective positions in terms of risk and return, offering a clear visual depiction of the trade-offs involved.
Each point on the graph corresponds to a specific strategy or portfolio, with its position reflecting the inherent balance between the expected return and the associated level of volatility. Portfolios or strategies that appear higher on the y-axis suggest higher expected returns, whereas their positioning along the x-axis indicates the level of risk, measured in terms of volatility, that investors would undertake.
This risk-reward graph is instrumental in providing investors with crucial insights into the performance dynamics of each strategy. It aids in making informed decisions by illustrating how different portfolios compare in terms of their potential returns for a given level of risk. Such a visual comparison is invaluable for strategic portfolio planning, helping investors to align their choices with their individual risk tolerance and return objectives.
Fig.14: Risk-Reward Analysis of Strategies and Portfolios
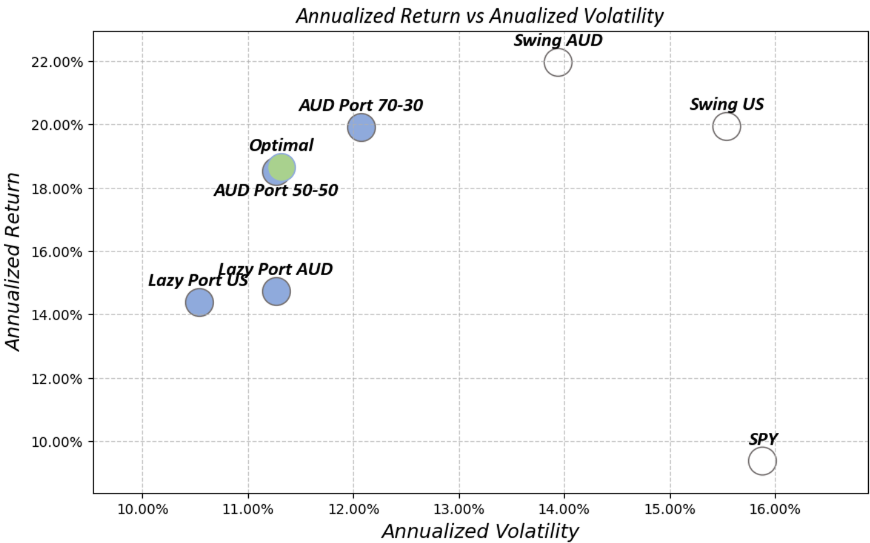
In our analysis of portfolio strategies utilizing AUD and USA ETFs, we observe notable parallels in performance, aligning with the expectation that the strategies would yield comparable results regardless of the ETFs' geographical focus.
Within the Swing strategy framework, the AUD variant demonstrates a commendable performance, reflecting a well-calibrated balance of risk and reward. This suggests that the AUD ETFs are competitive and effective in their own right, relative to their USA counterparts.
The investigation into the combined AUD portfolios, particularly the 70-30 and 50-50 blends, reveals that a strategic emphasis on the Swing component may present an attractive option for enhanced performance, with only a slight elevation in risk. Moreover, the 'Optimal' portfolio, which closely tracks the 50-50 blend, corroborates the concept of the efficient frontier, nearly achieving an exemplary risk-return equilibrium.
These findings are integral to the discourse on strategic allocation within portfolio management, emphasizing that the application of similar strategies across different ETF markets can yield akin outcomes.
Conclusion
In conclusion, this paper's exploration of Portfolio Optimization using AUD ETFs aims to extend the portfolio optimization strategies developed in our foundational research, "Optimizing Portfolio Performance: A Comprehensive Approach with Swing Trading, Asset Allocation, and Enhanced Lazy Portfolio," to the Australian financial context. Utilizing Australian ETFs that mirror their US counterparts, such as SPY.AX as a stand-in for SPY, we have sought to adapt these strategies to suit the Australian market's unique characteristics.
Through a meticulous backtesting regime, the research has demonstrated that when these proven strategies are implemented with AUD ETFs, they closely track the performance of the original US ETF-based strategies. This suggests that the success of the Swing and Lazy Portfolio strategies is not solely contingent upon the US market but can be effectively translated to Australian ETFs, highlighting the strategies' robust adaptability and relevance.
The study has closely examined two specifically constructed portfolios: the balanced Portfolio 50-50 and the more Swing-strategy-weighted Portfolio 70-30. Our findings show that these portfolios embody an effective translation of the original strategies, achieving a harmonious balance between risk and return. The Portfolio 50-50, in particular, stands out for its optimal alignment with the Efficient Frontier, substantiating the potential for strategic asset allocation to achieve superior risk-adjusted returns.
Our research culminates in the identification of the Optimal Efficient Frontier portfolio within the Australian ETF framework. This portfolio, consisting of a calculated blend of the Swing and Lazy Portfolio strategies, showcases a risk-return ratio that is not only theoretically sound but also practically attainable.
The implications of this study are significant, underscoring the versatility of ETFs and the efficacy of the Swing and Lazy Portfolio strategies beyond their American origins. It affirms the hypothesis that strategic investment principles are transferable across markets when the appropriate ETF equivalents are employed.
As ETF markets continue to globalize, this paper provides a valuable reference for investors seeking to apply established strategies in new contexts. It offers a testament to the universality of sound investment principles and contributes a meaningful chapter to the ongoing narrative of global investment strategy optimization.
Anexo 1: Formulas
Below are the formulas used to calculate the performance metrics:
Annual Return %: The annualized percentage return is a measure of the average annual rate of return on an investment over a specified time period.
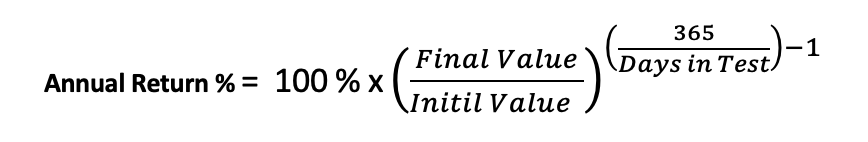
Max. system % drawdown: Maximum percentage decline in the value of a trading system from its highest point (peak) to the lowest subsequent point (trough) over a specified period.
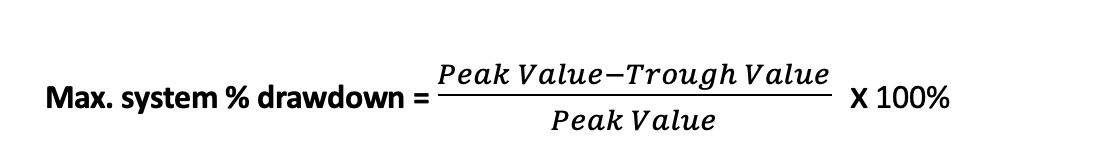
Where:
- Peak Value is the highest point in the value of the trading or investment system.
- Trough Value is the lowest subsequent point in the value of the system.
Recovery Factor: Assesses the ability of an investment or trading strategy to recover from losses. It is calculated using the following formula:
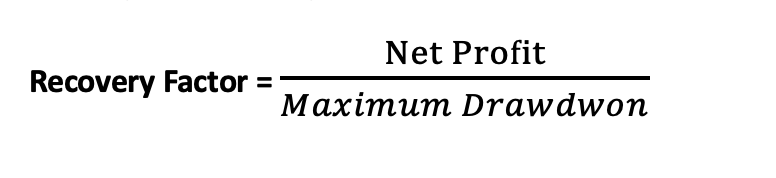
Profit Factor: Measures the profitability of a trading strategy. It is calculated using the following formula:
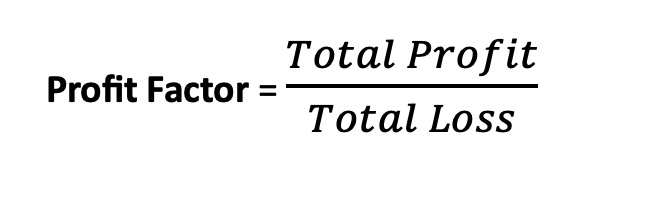
Payoff Ratio: Also known as the risk-reward ratio, is a financial metric used in investing to assess the potential return of an investment relative to the amount of risk undertaken.
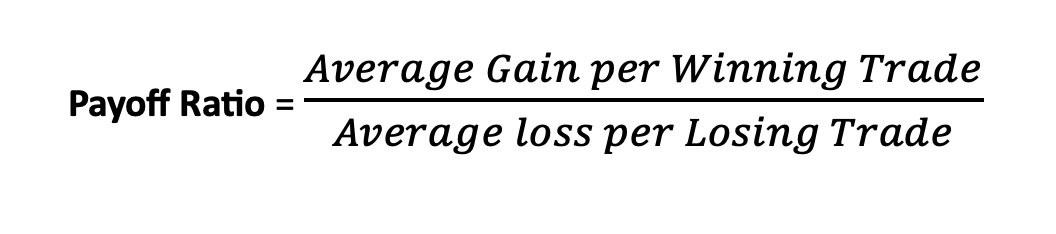
Sharpe Ratio: Is a measure of the risk-adjusted performance of a trading strategy. It helps investors evaluate the return of an investment relative to its risk.
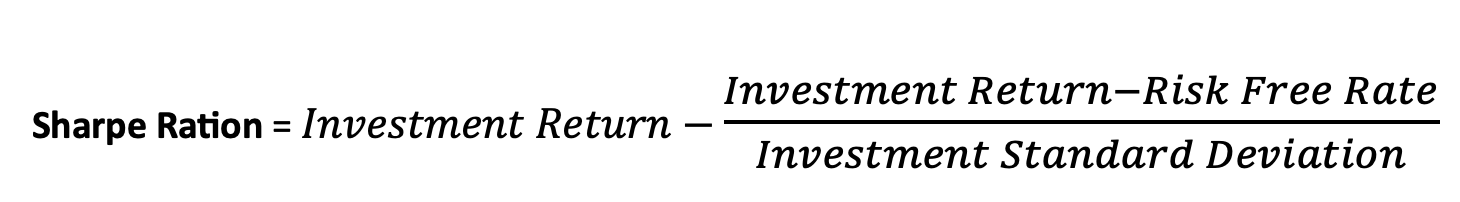
Where:
- Investment Return is the return of the investment or portfolio.
- Risk-Free RateRisk-Free Rate is the return on a risk-free investment.
- Investment Standard Deviation is the standard deviation of the Investment’s returns, which measures the volatility or risk of the portfolio.
Annualized Volatility: Is a measure of the variability of returns of an investment over a one-year period, expressed as a percentage. It is commonly used in finance to quantify the level of risk or uncertainty associated with an investment.
Calculated using Monthly returns:
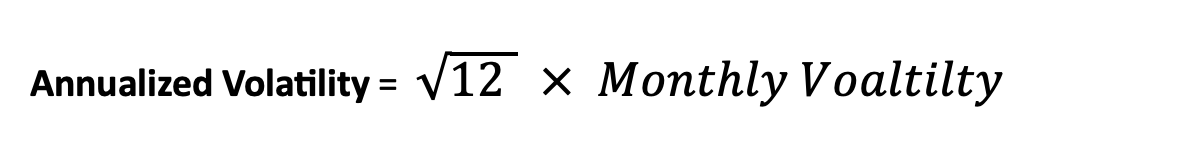
Where:
- Monthly Volatility is the standard deviation of monthly returns.
- 12 is the number of months in a year.
Ratio Sortino: Is a measure of risk-adjusted return that focuses on the downside risk of an investment. It is similar to the Sharpe Ratio, but it considers only the volatility of the downside. while the Sharpe Ratio considers total volatility (both upside and downside), the Sortino Ratio specifically looks at the downside risk, providing a more targeted measure for investors primarily concerned with minimizing losses. The Sortino Ratio can be useful in situations where protecting against downside risk is a critical factor in the investment strategy.